El objetivo de este articulo es explicar el Perceptrón y su utilización en la IA, así como el desarrollo con un ejemplo de código en Python mostrando un pseudocodigo para mostrar el funcionamiento y ejecución del Perceptrón.
Introducción
El perceptrón fue presentado en 1958 por Rosenblatt en la publicación “The perceptron: A probabilistic model for information storage and organization in the brain.”[1] El cual mostraba el uso mas simple de los Algoritmos ANN, Esto dereibo en diferentes técnicas que utilizan la base del perceptrón para el uso de algoritmos en redes neuronales.[2]
El Perceptrón está basado en el procesamiento de información de una única célula neuronal llamada neurona. Una neurona acepta señales de entrada, que transmiten la señal eléctrica al cuerpo celular. De manera similar, el Perceptrón recibe señales de entrada de ejemplos de datos de entrenamiento que ponderamos y combinamos en una ecuación lineal llamada activación.
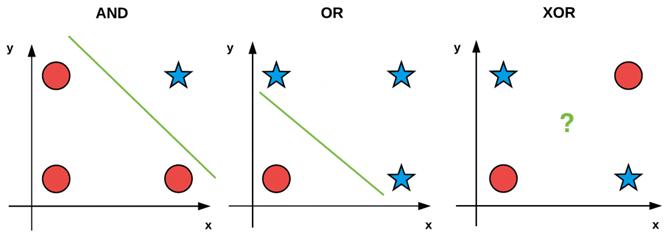
Para las técnicas de los algoritmos basadas en perceptrón Utilizamos las compuertas lógicas AND, OR y XOR, mostramos en la imagen 1 el modelo para cada uno de estos operadores
Imagen 1 Puertas lógicas.
Metodología
Para el algoritmo de entrenamiento del perceptrón utilizaremos 4 casos que incluyen el pseudocódigo de ejecución y los resultados medios con la función tiempo para demostrar la velocidad de ejecución.
Las pruebas realizadas serán:
Caso 1. Perceptrón simple con AND.
Caso 2. Perceptrón simple y descenso de gradiente con AND.
Caso 3. Perceptrón simple con OR.
Caso 4. Perceptrón simple y descenso de gradiente con OR.
Para simplificación iniciaremos con las pruebas de los casos 1 y 3, utilizando el código similar y cambiando las compuertas AND por OR.
Casos 1 y 3 Perceptrón simple con AND & OR
[1] https://psycnet.apa.org/doiLanding?doi=10.1037%2Fh0042519
[2] https://pyimagesearch.com/2021/05/06/implementing-the-perceptron-neural-network-with-python/
Codigo:
import numpy as np
import time
def predict(inputs, weights):
summation = np.dot(inputs, weights[1:]) + weights[0]
#print('summation:',summation)
return 1 if summation > 0 else 0
def train_perceptron(training_data, labels, learning_rate=0.01, epochs=100):
input_size = training_size = training_data.shape[1]
weights = np.random.rand(input_size +1) # +1 for bias term
#print(f'weights:', weights)
for _ in range(epochs):
for inputs, label in zip(training_data, labels):
prediction = predict(inputs, weights)
error = label - prediction
weights[1:] += learning_rate * error * inputs
weights[0] +=learning_rate * error
#print(f'weights en epoch:', weights, 'error:', error)
return weights
training_data = np.array([[2,3], [1,5], [3,4], [4,2]])
labels = np.array([1, 1 , 1, 0]) # clase 1: 1, clse 2: 0 Y deaseada
labels2 = np.array([1, 1 , 1, 0]) # clase 1: 1, clse 2: 0 Y deaseada
weights = train_perceptron(training_data, labels)
#datos prueba
startQ = time.time()
print('perceptron OR 1,1,1,0')
test_data = np.array([[1, 2], [5, 3]])
for data in test_data:
prediction = predict(data, weights)
if prediction == 1:
print(f"El punto {data} pertenece a la Clase 1.")
else:
print(f"El punto {data} pertence a la Clase 2.")
endQ = time.time()
t_ejecucion_Q = endQ - startQ
print('tiempo de ejecucion:', t_ejecucion_Q)
startQ = time.time()
print('perceptron AND 1,0,0,0')
test_data = np.array([[1, 2], [5, 3]])
for data in test_data:
prediction = predict(data, weights)
if prediction == 1:
print(f"El punto {data} pertenece a la Clase 1.")
else:
print(f"El punto {data} pertence a la Clase 2.")
endQ = time.time()
t_ejecucion_Q = endQ - startQ
print('tiempo de ejecucion:', t_ejecucion_Q)
Los resultados obtenidos son:
perceptron OR 1,1,1,0
El punto [1 2] pertenece a la Clase 1.
El punto [5 3] pertenece a la Clase 2.
tiempo de ejecucion: 0.0008504390716552734
perceptron AND 1,0,0,0
El punto [1 2] pertenece a la Clase 1.
El punto [5 3] pertenece a la Clase 2.
tiempo de ejecucion: 0.0018508434295654297
| Perceptrón OR 1,1,1,0 |
| El punto [1 2] pertenece a la Clase 1. |
| El punto [5 3] pertenece a la Clase 2. |
| tiempo de ejecución: 0.0008504390716552734 |
| Perceptrón AND 1,0,0,0 |
| El punto [1 2] pertenece ala Clase 1. |
| El punto [5 3] pertenece a la Clase 2. |
| tiempo de ejecución: 0.0018508434295654297 |
Casos 2 y 4 Perceptrón simple y descenso de gradiente con AND & OR
Pseudocódigo
import numpy as np
import time
def predict(row, weigths):
activation = weights[0]
for i in range(len(row)-1):
activation += weigths[i + 1] * row[i]
return 1 if activation >=0 else 0
def train_weights(train, l_rate=0.01, n_epoch=100):
weights = [0.0 for i in range(len(train[0]))]
for epoch in range(n_epoch):
sum_error = 0.0
for row in train:
prediction = predict(row, weights)
error = row[-1] - prediction
sum_error += error**2
weights[0] = weights[0] + l_rate * error
for i in range(len(row)-1):
weights[i + 1] = weights[i + 1] + l_rate * error * row[i]
return weights
dataset = np.array([[2,3,1], [1,5,0], [3,4,0], [4,2,0]])
dataset2 = np.array([[2,3,1], [1,5,1], [3,4,1], [4,2,0]])
#weights = [-0.1, 0.20653640140000007, -0.23418117710000003]
weights = train_weights(dataset)
labels = np.array([1, 0 , 1, 0]) # clase 1: 1, clse 2: 0 Y deaseada
startQ = time.time()
print('Perceptron Gradiante AND 1,0,0,0')
for row in dataset_test:
prediction = predict(row, weights)
if prediction == 1:
print(f"El punto {row} pertenece a la Clase 1.")
else:
print(f"El punto {row} pertence a la Clase 2.")
endQ = time.time()
t_ejecucion_Q = endQ - startQ
print('tiempo de ejecucion:', t_ejecucion_Q)
dataset_test = np.array([[1, 2], [5, 3]])
startQ = time.time()
print('Perceptron Gradiante OR 1,1,1,0')
for row in dataset_test:
prediction = predict(row, weights)
if prediction == 1:
print(f"El punto {row} pertenece a la Clase 1.")
else:
print(f"El punto {row} pertence a la Clase 2.")
endQ = time.time()
t_ejecucion_Q = endQ - startQ
print('tiempo de ejecucion:', t_ejecucion_Q)
Los resultados obtenidos son:
Perceptron Gradiante AND 1,0,0,0
El punto [1 2] pertenece a la Clase 1.
El punto [5 3] pertenece a la Clase 1.
tiempo de ejecucion: 0.0010912418365478516
Perceptron Gradiante OR 1,1,1,0
El punto [1 2] pertenece a la Clase 1.
El punto [5 3] pertenece a la Clase 1.
tiempo de ejecucion: 0.0005478858947753906
Conclusiones
Encontramos la utilidad del perceptrón para realizar funciones de clasificación por aprendizaje supervisado, este modelo para creación de algoritmos nos servirá como base para desarrollar sistemas mas complejos y con mayores capacidades.
Los resultados de las pruebas son los siguientes:
| Perceptron OR 1,1,1,0 |
| El punto [1 2] pertenece ala Clase 1. |
| El punto [5 3] pertence a la Clase 2. |
| tiempo de ejecucion: 0.0008504390716552734 |
| Perceptron AND 1,0,0,0 |
| El punto [1 2] pertenece ala Clase 1. |
| El punto [5 3] pertence a la Clase 2. |
| tiempo de ejecucion: 0.0018508434295654297 |
| Perceptron Gradiante AND 1,0,0,0 |
| El punto [1 2] pertenece a la Clase 1. |
| El punto [5 3] pertenece a la Clase 1. |
| tiempo de ejecucion: 0.0010912418365478516 |
| Perceptron Gradiante OR 1,1,1,0 |
| El punto [1 2] pertenece a la Clase 1. |
| El punto [5 3] pertenece a la Clase 1. |
| tiempo de ejecucion: 0.0005478858947753906 |
Para estos ejercicios encontramos el perceptrón por gradiente OR con la mejor velocidad de desempeño.
Referencias
- Referencia del libro “The perceptron: A probabilistic model for information storage and organization in the brain.” ttps://psycnet.apa.org/doiLanding?doi=10.1037%2Fh0042519
- Implementing the Perceptron Neural Network with Python https://pyimagesearch.com/2021/05/06/implementing-the-perceptron-neural-network-with-python/